Binary Tree Basics (Part 3) - Segment Tree

Concept
1. Structure
Basic Operations
Complete Code

Concept

A segment tree is a data structure commonly used for maintaining interval information.

Segment trees can perform operations like single-point modification, interval modification, and interval queries (such as interval sum, maximum value, minimum value) in time complexity.

Structure

A segment tree divides each interval of non-unit length into left and right sub-intervals recursively. It forms a tree structure where the entire segment is divided. The information of the interval is obtained by merging the information of the left and right sub-intervals. This data structure facilitates most interval operations.

Suppose we have an array . Let the root node of the segment tree be numbered , and we use an array to store the segment tree, where stores the value of the node with index in the segment tree.

The structure of this segment tree is as follows:

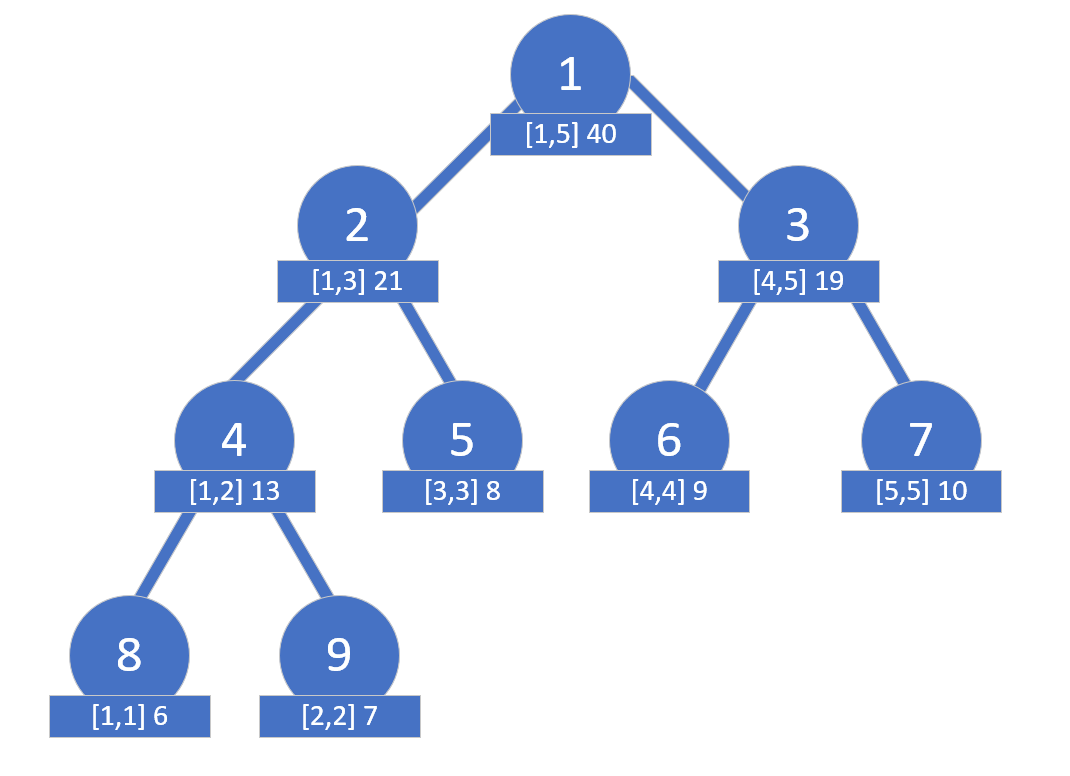
Segment Tree Structure

Here’s the corresponding code:

    vector<int> node; // Segment tree indexing starts from 1
    vector<int> nums; // Auxiliary for building the tree
    int N;

Basic Operations

Building the Segment Tree

For a node , its child nodes are numbered and . If node stores the interval , then node should store the interval , and similarly, node should store the interval . We can build the tree recursively. Here’s the code:

void build(int i, int l, int r) { // i represents the current node, l represents the left boundary, r represents the right boundary
    if (l == r) {
        node[i] = nums[l];
        return;
    }
    int mid = (l + r) / 2;
    build(2 * i, l, mid);
    build(2 * i + 1, mid + 1, r);
    node[i] = node[2 * i] + node[2 * i + 1];
}

Interval Query

If the query interval is , we can directly return . But if the query is , we need to merge the answers of and . Here’s the code:

int query(int i, int l, int r, int s, int t) { // i represents the current node, [l,r] is the query interval, [s,t] represents the interval covered by the current node
    if (l <= s && r >= t) // If [s,t] is a sub-interval of [l,r], directly return
        return node[i];
    int sum = 0, mid = (s + t) / 2; // Recursively query sub-intervals with intersections
    if (l <= mid) sum += query(2 * i, l, r, s, mid); // Recursively query left subtree
    if (r >= mid + 1) sum += query(2 * i + 1, l, r, mid + 1, t); // Recursively query right subtree
    return sum;
}

Interval Modification

Similar to interval queries, if there’s a containment relationship, we can directly add the value to be updated. If there’s an intersection, we perform recursive updates. Here’s the code:

void update(int i, int l, int r, int s, int t, int add) {
    if (l <= s && r >= t) { // If [s,t] is a sub-interval of [l,r], directly update
        node[i] += (t - s + 1) * add;
        return;
    }
    int mid = (s + t) / 2; // Recursively update sub-intervals with intersections
    if (l <= mid) update(2 * i, l, r, s, mid, add); // Recursively update left subtree
    if (r >= mid + 1) update(2 * i + 1, l, r, mid + 1, t, add); // Recursively update right subtree
    node[i] = node[2 * i] + node[2 * i + 1];
}

Lazy Propagation

When updating the interval of the array by adding , the updated segment tree structure becomes:

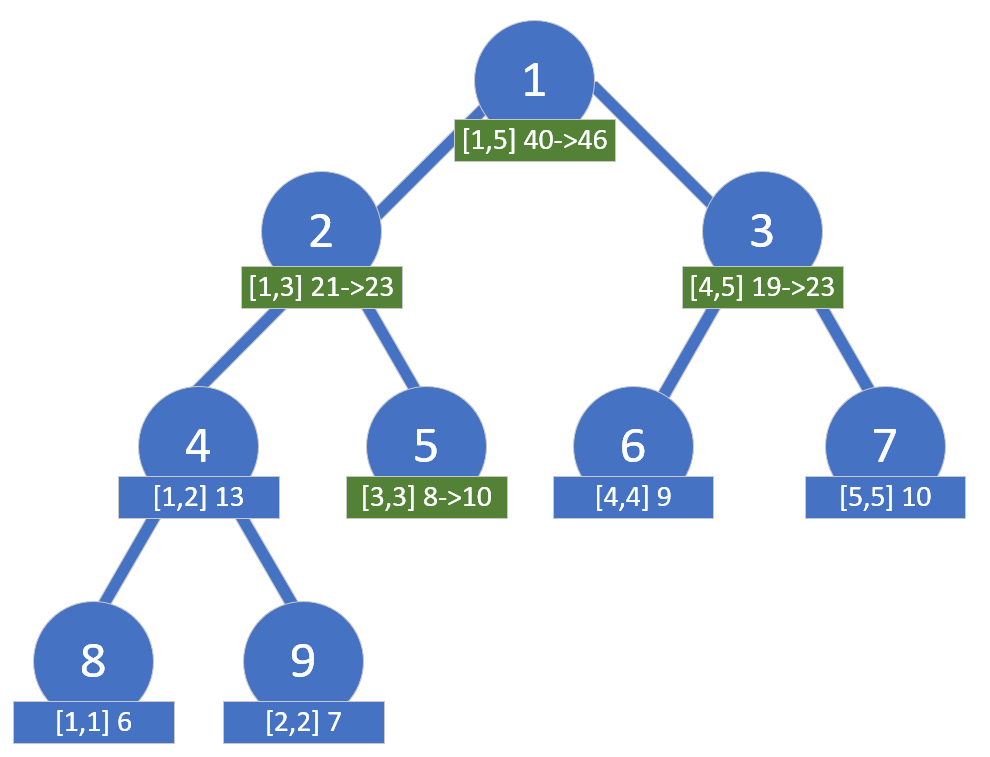
Segment Tree Lazy Propagation

We notice that when recursively updating, the process stops at node , leaving its two child nodes unchanged.

To handle this, we introduce lazy propagation. We mark the nodes where recursion ends with a flag. During the next query operation, we update the unprocessed child nodes. This flag is called a lazy tag. The effect of updating is as follows:

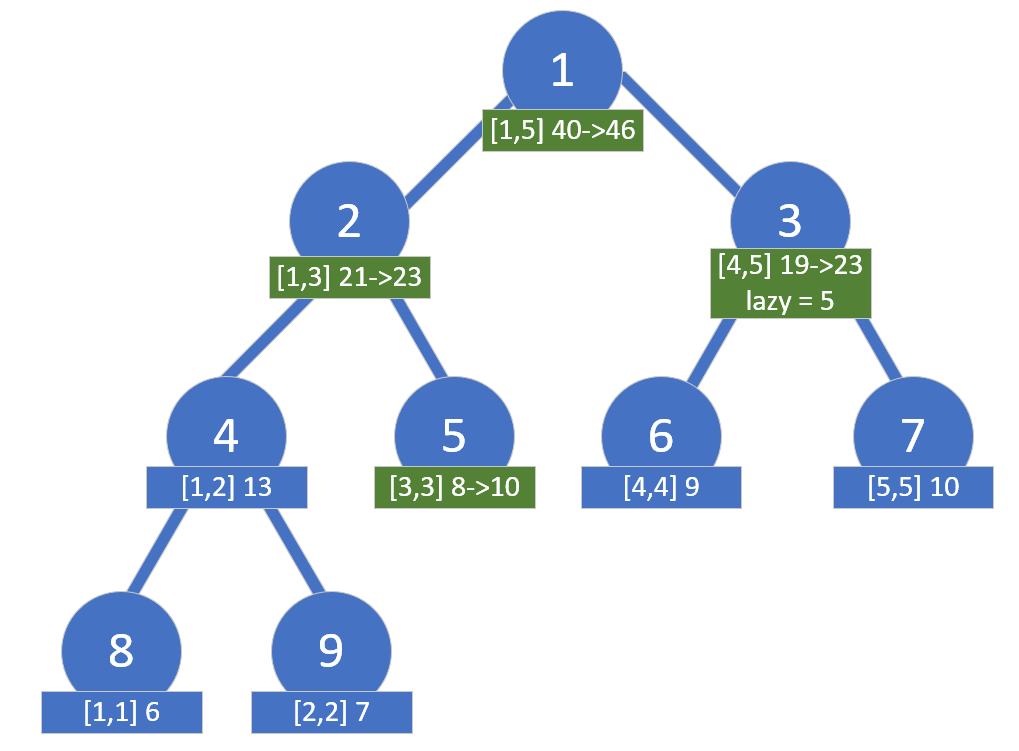
Segment Tree Lazy Propagation Update

And the effect after querying is as follows:

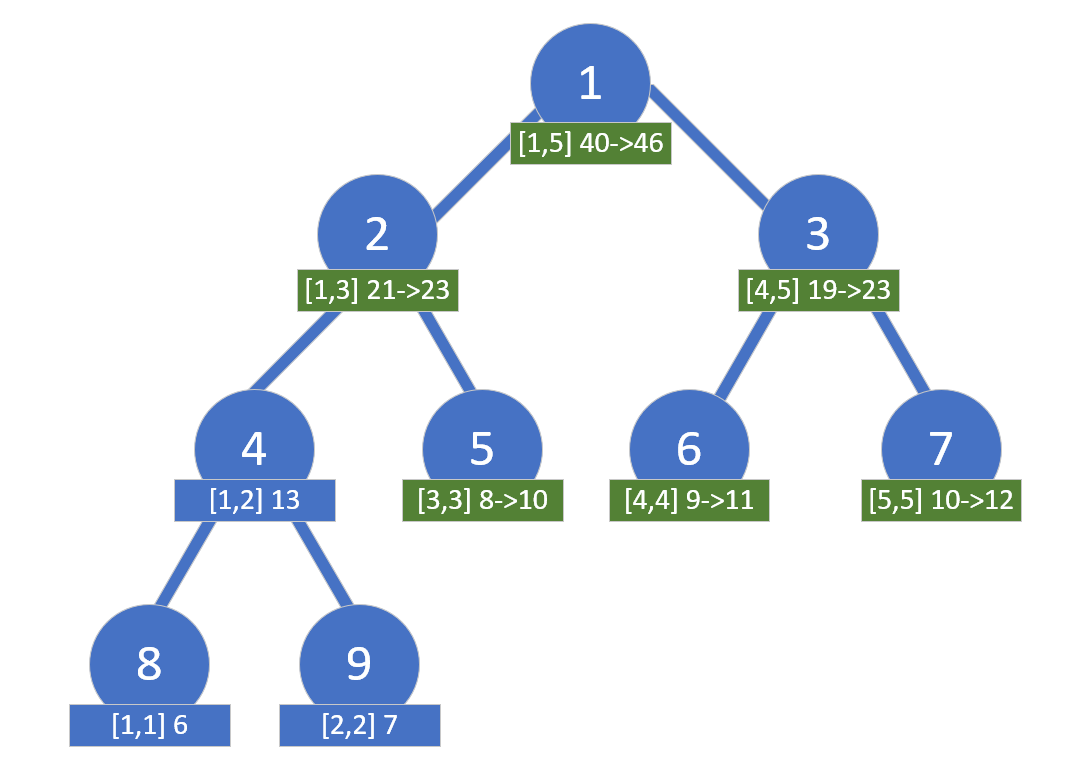
Segment Tree Lazy Propagation Query

We can use a vector<int> lazy to store the lazy tags. Here’s the lazy propagation code:

void push_down(int i, int l, int r) {
    if (!lazy[i])
        return;
    int mid = (l + r) / 2;
    lazy[2 * i] += lazy[i];
    lazy[2 * i + 1] += lazy[i];             // Propagate lazy tag down
    node[2 * i] += (mid - l + 1) * lazy[i];
    node[2 * i + 1] += (r - mid) * lazy[i]; // Add the value of the lazy tag to the child nodes
    lazy[i] = 0;
}

Then call push_down() in the query and update functions accordingly.

Complete Code

class SegmentTree {
public:
    vector<int> node; // Segment tree indexing starts from 1
    vector<int> lazy; // Lazy tags
    vector<int> nums; // Auxiliary for building the tree
    int N = 1;

    SegmentTree(vector<int> nums, int n) : node(n + 1, 0), lazy(n + 1, 0), nums(nums) {}

    void build(int i, int l, int r) { // i represents the current node

, l represents the left boundary, r represents the right boundary
        N++;
        if (l == r) {
            node[i] = nums[l - 1];
            return;
        }
        int mid = (l + r) / 2;
        build(2 * i, l, mid);
        build(2 * i + 1, mid + 1, r);
        node[i] = node[2 * i] + node[2 * i + 1];
    }

    void push_down(int i, int l, int r) {
        if (!lazy[i])
            return;
        int mid = (l + r) / 2;
        lazy[2 * i] += lazy[i];
        lazy[2 * i + 1] += lazy[i];             // Propagate lazy tag down
        node[2 * i] += (mid - l + 1) * lazy[i];
        node[2 * i + 1] += (r - mid) * lazy[i]; // Add the value of the lazy tag to the child nodes
        lazy[i] = 0;
    }

    int query(int i, int l, int r, int s, int t) { // i represents the current node, [l,r] is the query interval, [s,t] represents the interval covered by the current node
        if (l <= s && r >= t) // If [s,t] is a sub-interval of [l,r], directly return
            return node[i];
        push_down(i, s, t);
        int sum = 0, mid = (s + t) / 2; // Recursively query sub-intervals with intersections
        if (l <= mid) sum += query(2 * i, l, r, s, mid); // Recursively query left subtree
        if (r >= mid + 1) sum += query(2 * i + 1, l, r, mid + 1, t); // Recursively query right subtree
        return sum;
    }

    void update(int i, int l, int r, int s, int t, int add) {
        if (l <= s && r >= t) { // If [s,t] is a sub-interval of [l,r], directly update
            lazy[i] += add;
            node[i] += (t - s + 1) * add;
            return;
        }
        push_down(i, s, t);
        int mid = (s + t) / 2; // Recursively update sub-intervals with intersections
        if (l <= mid) update(2 * i, l, r, s, mid, add); // Recursively update left subtree
        if (r >= mid + 1) update(2 * i + 1, l, r, mid + 1, t, add); // Recursively update right subtree
        node[i] = node[2 * i] + node[2 * i + 1];
    }
};