Using the ray-casting algorithm to determine whether a point is inside a polygon

Introduction

In computational geometry, determining whether a point lies inside a polygon is a common problem. Today, I needed to use this functionality in an actual project and chose the Ray Casting Algorithm to perform this determination. This article will detail the issues I encountered during implementation and their solutions, as well as share the relevant code.

Overview of the Ray Casting Algorithm

The Ray Casting Algorithm is a classic method for determining whether a point is inside a polygon. The basic idea is to cast a ray from the target point in any direction and count the number of times the ray intersects with the edges of the polygon. If the number of intersections is odd, the point is inside the polygon; if it is even, the point is outside.

Initial Implementation

When implementing the Ray Casting Algorithm, I primarily referenced a blog post from the Tencent Cloud Developer Community: Determining if a Point is Inside a Polygon Using the Ray Casting Method. Following the approach outlined in the blog, I wrote the following Python code:

def pointInPolygon(self, x, y):
    edgesX = self.polyX.copy()
    edgesY = self.polyY.copy()
    edgesX.append(edgesX[0])
    edgesY.append(edgesY[0])
    assert len(edgesX) == len(edgesY)
    sinsc = 0  # Intersection count
    for i in range(len(edgesX) - 1):  # Iterate through all edges
        startPoint = (edgesX[i], edgesY[i])
        endPoint = (edgesX[i + 1], edgesY[i + 1])
        if isRayIntersectsSegment((x, y), startPoint, endPoint):
            sinsc += 1  # Increment intersection count
    return True if sinsc % 2 == 1 else False

This code follows the logic of the original blog post: it iterates through each edge of the polygon, determines whether the ray intersects with that edge, and finally decides the position of the point based on the parity of the intersection count.

Testing and Problem Discovery

To verify the correctness of the code, I tested it with multiple cases on Nowcoder:

During testing, I found that the code failed some test cases. To better understand the issue, I used Python to draw diagrams of the failing cases:

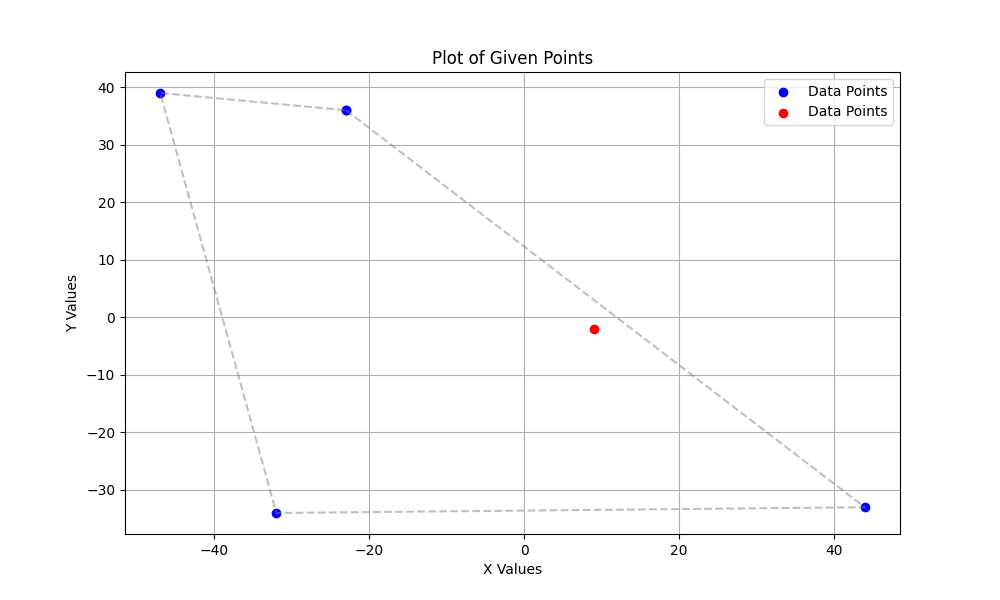
Diagram

Upon analyzing the diagram, I discovered that the original author included the following condition in the isRayIntersectsSegment function to perform potential pruning:

if s_poi[0] < poi[0] and e_poi[1] < poi[1]:  # Segment is to the left of the ray
    return False

However, this part of the code has a logical flaw: merely checking if the x-coordinate of the segment’s starting point is less than the target point’s x-coordinate and the y-coordinate of the segment’s ending point is less than the target point’s y-coordinate does not ensure that the segment is entirely to the left of the ray. For example, the counterexample in the diagram proves this point.

Code Correction

To fix the above issue, I enhanced the pruning conditions by adding checks for s_poi[1] and e_poi[0]. The modified isRayIntersectsSegment function is as follows:

def isRayIntersectsSegment(pointOfInterest, startPoint, endPoint):  # [x, y] [lng, lat]
    # Inputs: point to check, segment start point, segment end point, all in [lng, lat] format arrays
    if startPoint[1] == endPoint[1]:  # Exclude cases where the segment is parallel or coincides with the ray, or if the segment endpoints coincide
        return False
    if startPoint[1] > pointOfInterest[1] and endPoint[1] > pointOfInterest[1]:  # Segment is above the ray
        return False
    if startPoint[1] < pointOfInterest[1] and endPoint[1] < pointOfInterest[1]:  # Segment is below the ray
        return False
    if startPoint[1] == pointOfInterest[1] and endPoint[1] > pointOfInterest[1]:  # Intersection is at the lower endpoint of the starting point
        return False
    if endPoint[1] == pointOfInterest[1] and startPoint[1] > pointOfInterest[1]:  # Intersection is at the lower endpoint of the ending point
        return False
    if (startPoint[0] < pointOfInterest[0]
            and startPoint[1] < pointOfInterest[1]
            and endPoint[0] < pointOfInterest[0]
            and endPoint[1] < pointOfInterest[1]
    ):
        return False
    # Calculate the x-coordinate of the intersection point
    xIntersection = endPoint[0] - (endPoint[0] - startPoint[0]) * (endPoint[1] - pointOfInterest[1]) / (endPoint[1] - startPoint[1])
    if xIntersection < pointOfInterest[0]:  # Intersection point is to the left of the ray's origin
        return False
    return True  # In other cases, the ray intersects with the segment

In the newly added pruning conditions, I included checks for the segment’s ending point’s x-coordinate and the starting point’s y-coordinate to ensure that the segment is indeed to the left of the ray, thereby avoiding misjudgments.

Test Results

After making the above corrections, all test cases passed, proving that the revised algorithm is more robust and accurate.

Conclusion

In the process of implementing the Ray Casting Algorithm to determine whether a point is inside a polygon, handling the details meticulously is crucial. Although the original algorithm performs well in most scenarios, it can produce errors in certain edge cases. By thoroughly analyzing the test cases and optimizing the pruning conditions, I ultimately achieved a reliable point-in-polygon determination algorithm.

Despite some flaws in the initial code, through debugging and improvements, the desired outcome was achieved. I hope this article can provide reference and assistance to developers with similar needs.