1. Introduction
   1. Definition of Binary Tree
   2. Basic Forms
   3. Special Types
   4. Related Terminology
   5. Properties
2. Implementing Binary Trees in C++
   1. Sequential Storage of Binary Trees
      1. Implementation Code
   2. Linked Storage of Binary Trees
      1. Implementation Code
   3. Recursive Traversal of Binary Trees
      1. Preorder Traversal (DLR)
      2. Inorder Traversal (LDR)
      3. Postorder Traversal (LRD)

Introduction

A binary tree is a crucial type of tree structure. Many data structures abstracted from practical problems often take the form of binary trees. Even general trees can be easily converted into binary trees, and the storage structure and algorithms for binary trees are relatively simple. Hence, binary trees are particularly important. The defining characteristic of a binary tree is that each node can have at most two child nodes, with a distinction between left and right.

Definition of Binary Tree

A binary tree is a type of ordered tree in which the degree of each node is at most 2. It is the simplest and most important tree structure. The recursive definition of a binary tree states that a binary tree is either an empty tree or a tree formed by a root node and two disjoint, mutually exclusive binary trees called the left subtree and the right subtree.

Basic Forms

• Empty binary tree
• Binary tree with only one root node
• Binary tree with only a left subtree of the root node
• Binary tree with only a right subtree of the root node
• Complete binary tree with both left and right subtrees of the root node

  Special Types

• Full binary tree: A tree where each node has either 0 or 2 children, and nodes with 0 children are at the same level.
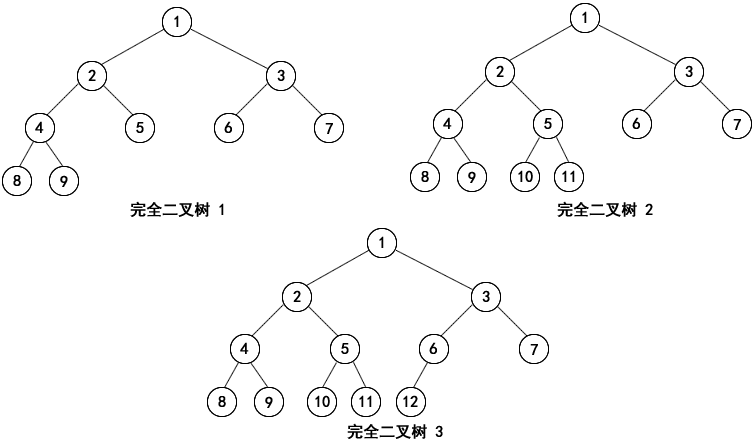
• Complete binary tree: A binary tree of depth k where each node is in the same level as the nodes of a full binary tree of depth k, numbered from 1 to n.

  Related Terminology

• Node: Contains a data element and information pointing to child subtrees.
• Node degree: The number of child subtrees a node has.
• Leaf node: Also known as a terminal node, it has no child subtrees or has a degree of 0.
• Branch node: Also known as a non-terminal node, it has a degree greater than 0.
• Tree degree: The maximum degree among all nodes in the tree.
• Node level: Starting from the root node, where the root node is at level 0, its children are at level 1, and so on.
• Tree depth: Also known as the height of the tree, it is the maximum level among all nodes in the tree.
• Ordered tree: If the subtrees of a tree have a specific sequence, the tree is ordered.
• Unordered tree: If the subtrees of a tree have no specific sequence, the tree is unordered.
• Forest: A collection of m (m≥0) disjoint trees. Removing the root node of a non-empty tree turns it into a forest, where each tree consists of the original root node’s subtrees.

  Properties

• A binary tree’s ith level can have at most nodes .
• A binary tree of depth k can have at most nodes .
• For a binary tree with n nodes, if the number of nodes with a degree of 0 is and with a degree of 2 is , then .
• Full binary tree theorem: The number of leaf nodes in a non-empty full binary tree equals the number of internal nodes .
• Corollary of full binary tree theorem: In a binary tree with n nodes, the number of null subtrees equals .
• The height of a complete binary tree with n nodes is , and the depth is .

Implementing Binary Trees in C++

Sequential Storage of Binary Trees

We can use an array to store all the nodes. The root node is stored at index 0, and its left child is stored at index $20+120+22i+12i+2$, respectively.

Implementation Code

typedef int BinaryTree[MAX];
void CreateBinaryTree(BinaryTree tree, int i) {
    if (i >= MAX) return;
    int input;
    cin >> tree[i];
    CreateBinaryTree(tree,2*i+1);
    CreateBinaryTree(tree,2*i+2);
}

Linked Storage of Binary Trees

Sequential storage is generally suitable for complete binary trees. Typically, we use linked storage to represent binary trees.

Implementation Code

typedef struct Node {
    int data;                     // Data
    struct Node *lchild, *rchild; // Left and right subtrees
} * BinaryTree, BtNode;

void CreateBinaryTree(BinaryTree &tree) {
    int input;
    cin >> input;
    if (input == -1) {
        tree = NULL;
        return;
    }
    tree = new BtNode;
    tree->data = input;
    CreateBinaryTree(tree->lchild);
    CreateBinaryTree(tree->rchild);
}

Recursive Traversal of Binary Trees

Preorder Traversal (DLR)

If the binary tree is empty, do nothing. Otherwise:

1. Visit the current node.
2. Traverse the left subtree in preorder.
3. Traverse the right subtree in preorder.

void DLR(BinaryTree tree) {
    if (tree) {
        cout << tree->data << endl;
        DLR(tree->lchild);
        DLR(tree->rchild);
    }
}

Inorder Traversal (LDR)

If the binary tree is empty, do nothing. Otherwise:

1. Traverse the left subtree in inorder.
2. Visit the current node.
3. Traverse the right subtree in inorder.

void LDR(BinaryTree tree) {
    if (tree) {
        LDR(tree->lchild);
        cout << tree->data << endl;
        LDR(tree->rchild);
    }
}

Postorder Traversal (LRD)

If the binary tree is empty, do nothing. Otherwise:

1. Traverse the left subtree in postorder.
2. Traverse the right subtree in postorder.
3. Visit the current node.

void LRD(BinaryTree tree) {
    if (tree) {
        LRD(tree->lchild);
        LRD(tree->rchild);
        cout << tree->data << endl;
    }
}